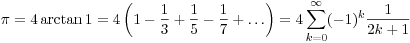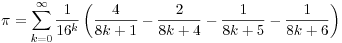
The first term is 3.1333, and very shortly (by k=4) you are well past 3.14159 in accuracy. In fact this formula, in octal, produces the digits of pi way out without needing to know all the previous terms. Current issue (as of 8/2013) of the Notices of the American Mathematical Society, and it is called a BPP formula.
What I like about this sort of formula is that it is easy to program on a calculator and you get the advantages of sophisticated analysis. You are participating in what is called "experimental mathematics." BPP comes from the PSLQ algorithm.
There are many other series that express pi, the usual ones being something like arctan 1= pi/4, and you use the series for the arctan. But here, to get a certain accuracy, you need to add up all the relevant terms up to some k